Inpainting
Module for inpainting images, mainly used for the following:
interpolation of holes in the images
seamless cloning
removal of harsh transitions between image borders for cross removal in the power spectrum
Power Spectrum Cross Removal
The helper function for the removal of the cross in the power spectrum is
prepare_border_smoothing(). For details see [Moisan, 2011].
Our implementation, which uses the 2-step forward/backward gradient to get the
Laplacian in create_inpaint_pipeline() makes the “v” field slightly
different than in the paper (defined in [Moisan, 2011] below eq.
11). The right/bottom border is equal to “v” from the paper but the left/top
border are True Laplacian values. Nevertheless, the other side does get inside,
so the filtering result is very similar. How is it similar and different:
g_forw( 0) = f(1) - f( 0)
g_forw(-1) = f(0) - f(-1)
# This is different from the paper
g_back( 0) = g_forw( 0) - g_forw(-1) = -2f(0) + f(1) + f(-1)
# After the forward pass, the gradient field is set to zeros everywhere except the borders.
# This is equivalent to the paper
g_back(-1) = g_forw(-1) - g_forw(-2) = g_forw(-1) - 0 = f(0) - f(-1)
On the top of that, we use the fact that:
![\begin{align}
g(x, y)
& = f(x, y) - \mathcal{F}^{-1} \left\{
\frac{\mathcal{F}
\left[
\frac{\partial}{\partial x}
\left(
\left( \frac{\partial}{\partial x} f(x, y) \right) m(x, y)
\right)
+ \frac{\partial}{\partial y}
\left(
\left( \frac{\partial}{\partial y} f(x, y) \right) m(x, y)
\right)
\right]}
{L(u, v)} \right\} \\
& = \mathcal{F}^{-1}
\left\{
\frac{\mathcal{F}
\left[
\frac{\partial}{\partial x}
\left(
\left(
\frac{\partial}{\partial x} f(x, y)
\right) \left( 1 - m(x, y) \right)
\right)
+ \frac{\partial}{\partial y}
\left(
\left(
\frac{\partial}{\partial y} f(x, y)
\right) \left( 1 - m(x, y) \right)
\right)
\right]}
{L(u, v)}
\right\} \\
& = \mathcal{F}^{-1}
\left\{
\frac{\mathcal{F}
\left[
\frac{\partial}{\partial x}
\left( \frac{\partial}{\partial x} f(x, y) \right)
+ \frac{\partial}{\partial y}
\left( \frac{\partial}{\partial y} f(x, y) \right)
\right]} {L(u, v)}
- \frac{\mathcal{F}
\left[
\frac{\partial}{\partial x}
\left(
\left( \frac{\partial}{\partial x} f(x, y) \right) m(x, y)
\right)
+ \frac{\partial}{\partial y}
\left(
\left( \frac{\partial}{\partial y} f(x, y) \right) m(x, y)
\right)
\right]} {L(u, v)}
\right\} \\
& = \mathcal{F}^{-1}
\left\{
\mathcal{F} \left[ f(x, y) \right]
- \frac{\mathcal{F}
\left[
\frac{\partial}{\partial x}
\left(
\left( \frac{\partial}{\partial x} f(x, y) \right) m(x, y)
\right)
+ \frac{\partial}{\partial y}
\left(
\left( \frac{\partial}{\partial y} f(x, y) \right) m(x, y)
\right)
\right]} {L(u, v)}
\right\}
\end{align}](../_images/math/603f8b4495235198ec2fdf26e40c2c0cdf5cb72b.png)
to remove the need of the subtraction from the original image, thus, we implement Eq. (2)
instead of Eq. (1). 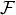 is the Fourier transform,
is the Fourier transform, 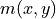 is the binary
mask which specifies which pixels in the gradient will be zeroed,
is the binary
mask which specifies which pixels in the gradient will be zeroed, 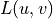 is the Laplace
operator in Fourier space.
is the Laplace
operator in Fourier space.
Inpaint Module
- tofu.inpaint.create_inpaint_pipeline(args, graph, processing_node=None)[source]
Create tasks needed for inpainting and connect them. The pipeline has three inputs and one output, which is the inpainted image. Based on [Morel et al., 2012].
- tofu.inpaint.prepare_border_smoothing(padded_width, padded_height)[source]
The use case here is mainly the removal of the cross at (0, 0) in the power spectrum by masking out the borders of the image, i.e. the gradients are forced to go to zeros at the borders and thus removing the sharp transitions when we consider the periodicity assumed by the DFT. padded_width and padded_height are the width and height of the FFT-padding, not the original image shape. One should use `mirrored_repeat’ padding mode on the input images to get the FFT-padded image, compute the mask here and use it for inpainting.